Chapter 4: QUBO as a Graph

(Intuition Without Math Fear)

Goal of this chapter

• Build intuition for QUBO without heavy math
• Understand nodes and connections (graph view)
• See why QUBO works so well for complex problems

---

1. Why look at QUBO as a Graph?

So far, QUBO looked like a math formula:

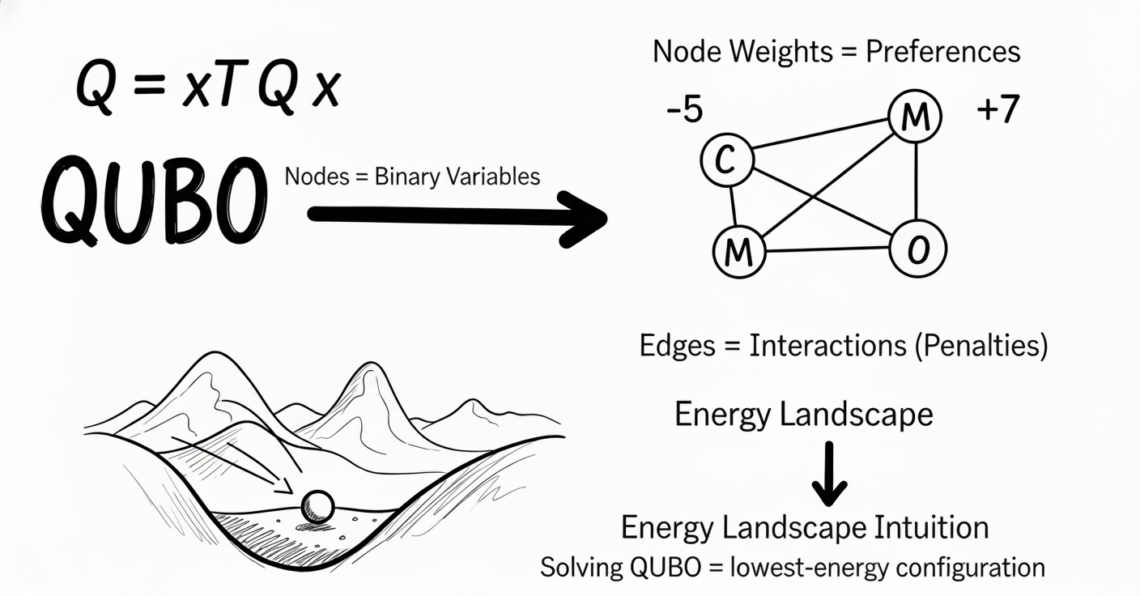
Q = xᵀ Q x

But behind the math, QUBO is really a graph problem.

Thinking in graphs helps you:

• visualize the problem
• understand interactions between choices
• debug bad QUBO models

---

2. Nodes = Binary Variables

Every binary variable becomes a node.

Example:

C = choose Coke
M = choose Milk Tea
O = choose Orange Juice

Graph view:

• Node C
• Node M
• Node O

Each node can be:

• OFF (0)
• ON (1)

---

3. Node Weights = Preferences

If a variable has a linear term, it becomes a node weight.

Example objective:

-5C + 7M + 0O

Graph interpretation:

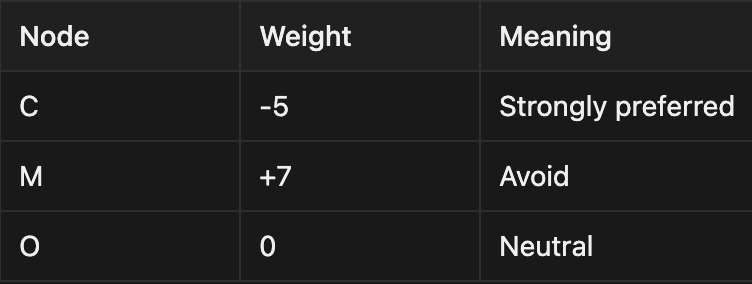
Turning ON a node adds its weight to the total cost.

---

4. Edges = Interactions (Penalties)

When two variables multiply each other, they form an edge.

Example penalty:

CM

Graph meaning:

• If both C and M are ON, add penalty
• If one or both are OFF, no penalty

Edges enforce rules like:

• “Don’t pick both”
• “These two conflict”

---

5. Example: “Don’t Choose Both”

Rule:

• You cannot choose Coke and Milk Tea together

QUBO penalty:

CM

Graph view :

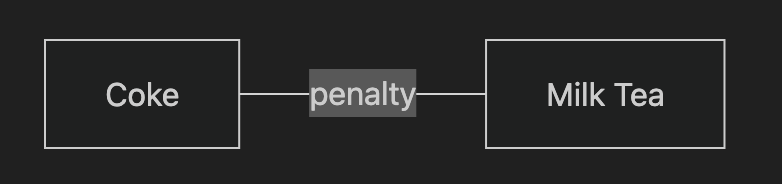
• Node C (Coke) and node M (Milk Tea) represent choices
• The edge means: if both are ON → penalty is added

If both nodes are ON → penalty is added.

---

6. Exactly-One Constraint as a Graph

Constraint:

(C + M + O - 1)²

Expanded form:

C + M + O
+ 2(CM + CO + MO)
- 2(C + M + O)
+ 1

Graph view:

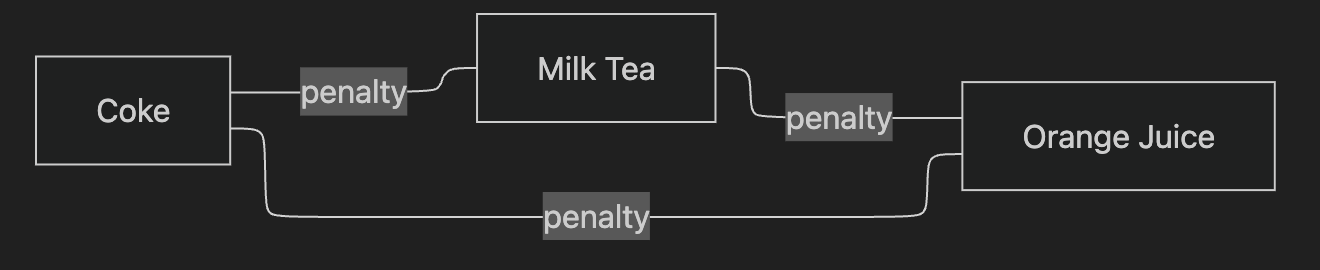
• Each node = one choice
• Every pair is connected
• Edges penalize choosing multiple items

This is why exactly-one constraints create fully connected graphs.

---

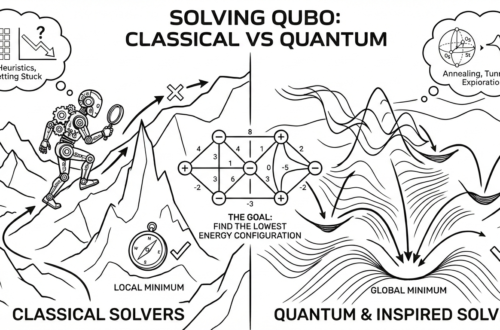
7. Energy Landscape Intuition

Think of QUBO as a landscape:

• High hills = bad solutions
• Deep valleys = good solutions

The solver is like a ball rolling downhill.

• Penalties create steep cliffs
• Preferences create slopes

The lowest valley = best solution.

---

8. Why Graph View Matters in Practice

Graph intuition helps you:

• reduce unnecessary connections
• tune penalty weights
• understand solver performance

Sparse graphs → easier to solve

Dense graphs → harder but expressive

---

9. Key Takeaways

• QUBO = graph + weights
• Nodes = choices
• Edges = interactions / penalties
• Solving QUBO = finding lowest-energy configuration

---

Keep in mind this

Nodes want to turn ON

Edges tell them who they can’t be ON with

If this makes sense, the next step inChapter 5: Solving QUBO will feel much more natural.